실전 알고리즘 0x18강

실전알고리즘 공부

실전 알고리즘 0x18강 - 그래프

diligent_gideok 2022. 6. 1. 04:01

그래프

[ 정의와 표현법 ]

- 정의 : 그래프 = 정점과 간선으로 이루어진 자료구조

- 차수 : 각 정점에 대해서 간선으로 연결된 이웃한 정점의 개수

- 무방향 그래프 or 방향 그래프( outdegree, indegree )

- 사이클 : 임의의 한 점에서 출발해 자기 자신으로 돌아올 수 있는 경로

- 순환 그래프 or 비순환 그래프

- 완전 그래프 or 연결 그래프

- 그래프는 꼭 연결되어 있어야 할 필요도 없고 두 정점 사이에 간선이 반드시 1개 이하일 필요도, 또 간선이 반드시 서로 다른 두 정점을 연결해야 할 필요도 없다.

- 단순 그래프 : 두 정점 사이의 간선이 1개 이하이고 루프가 존재하지 않는 그래프

- 표현법 1 - 인접 행렬 ( 연결 여부를 O(1)에 확인 가능, 공간은 O(V^2) 필요 )

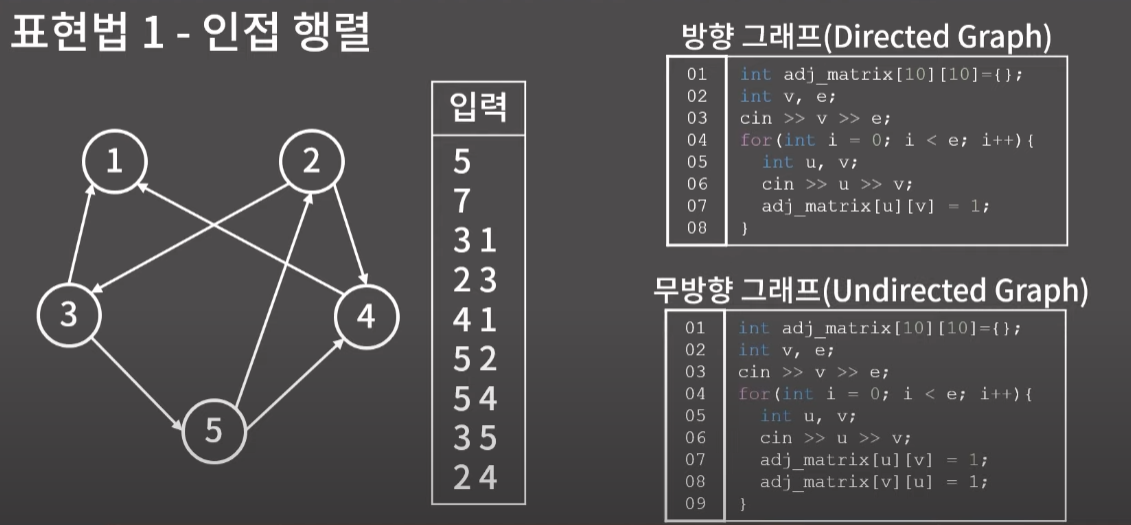
- 표현법 2 - 인접 리스트 ( O(V+E)의 공간이 필요, 연결리스트 말고 vector로 구현한다 )

- STL을 사용하지 못한다면 잘못 구현하면 V*V의 공간을 사용하게 된다. 그렇기 때문에 vector이나 list 같은 연결 리스트 기능을 하는 클래스를 만들어서 쓰는 방법으로 구현한다. 이 방법은 실수할 가능성이 있기 때문에 다음 코드처럼 구현한다.

int edge[10][2];
int deg[10]; // 각 정점의 outdegree
int* adj[10];
int idx[10]; // adj[i]에서 새로운 정점을 추가할 때의 위치
int main() {
	int v, e;
	cin >> v >> e;
	for (int i = 0; i < e; i++) {
		cin >> edge[i][0] >> edge[i][1];
		deg[edge[i][0]]++;
	}
	for (int i = 1; i <= v; i++)
		adj[i] = new int[deg[i]];
	for (int i = 0; i < e; i++) {
		int u = edge[i][0], v = edge[i][1];
		adj[u][idx[u]] = v;
		idx[u]++;
	}
}

// 무방향 그래프
int edge[10][2];
int deg[10]; // 각 정점의 outdegree
int* adj[10];
int idx[10]; // adj[i]에서 새로운 정점을 추가할 때의 위치
int main() {
	int v, e;
	cin >> v >> e;
	for (int i = 0; i < e; i++) {
		cin >> edge[i][0] >> edge[i][1];
		deg[edge[i][0]]++; deg[edge[i][1]]++;
	}
	for (int i = 1; i <= v; i++)
		adj[i] = new int[deg[i]];
	for (int i = 0; i < e; i++) {
		int u = edge[i][0], v = edge[i][1];
		adj[u][idx[u]] = v;
		idx[u]++;
		adj[v][idx[v]] = u;
		idx[v]++;
	}
}

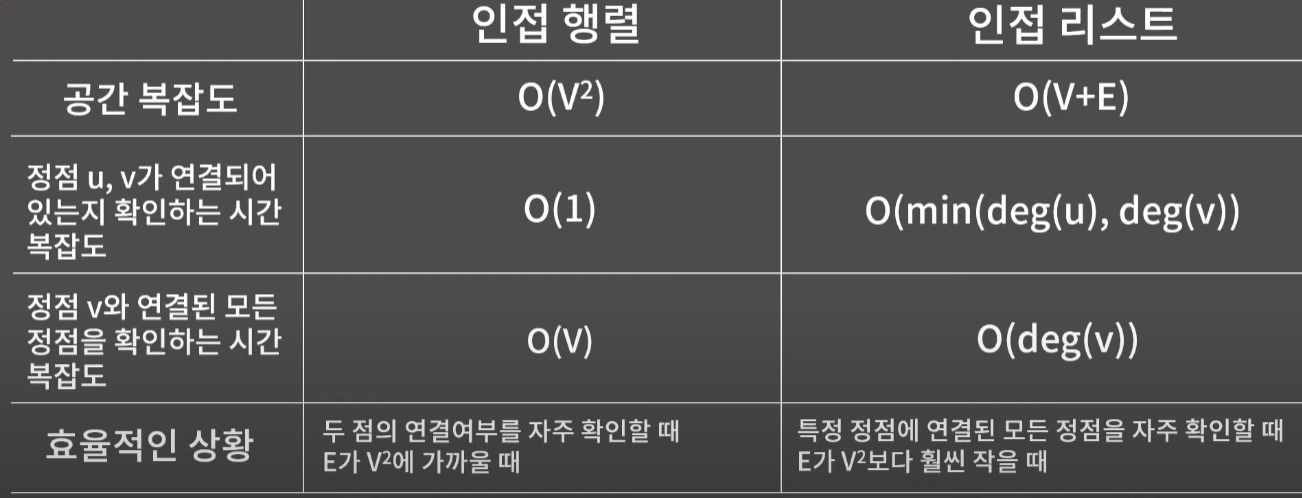
- 보통 인접 행렬보다 인접 리스트들로 구현하는 경우가 많다.

[ BFS ]

- 그래프에서 너비를 우선으로 방문하는 알고리즘

1. 시작하는 정점을 큐에 넣고 방문했다는 표시를 남김

2. 큐에서 정점을 꺼내어 그 정점과 연결된 모든 정점들에 대해 3번을 진행

3. 해당 정점을 이전에 방문했다면 아무 것도 하지 않고, 처음으로 방문했다면 방문했다는 표시를 남기고 해당 칸을 큐에 삽입

4. 큐가 빌 때 까지 2번을 반목

모든 정점이 큐에 최대 1번씩 들어가므로 인접 리스트에서 O(V+E), 인접 행렬에서 O(V^2)의 시간 복잡도.

- 그래프에서는 시간 복잡도에 E가 포함된다. (ex. V=2,000이고 완전 그래프이면 E=2,000,000이고 BFS를 1000번 돌리면 O(1000V)가 아니라 O(1000(V+E))여서 시간 초과가 발생한다.

- BFS 예시 코드 1 : 연결 그래프에서의 순회

#include <bits/stdc++.h>
using namespace std;


vector<int> adj[10];
bool vis[10];
void bfs() {
	queue<int> q;
	q.push(1);
	vis[1] = true;
	while (!q.empty()) {
		int cur = q.front();
		q.pop();
		cout << cur << ' ';
		for (auto nxt : adj[cur]) {
			if (vis[nxt]) continue;
			q.push(nxt);
			vis[nxt] = true;
		}
	}
}

- BFS 예시 코드 2 : 연결 그래프에서 1번 정점과의 거리

vector<int> adj[10];
int dist[10];
void bfs() {
	fill(dist, dist + 10, -1);
	queue<int> q;
	q.push(1);
	vis[1] = 0;
	while (!q.empty()) {
		int cur = q.front();
		q.pop();
		for (auto nxt : adj[cur]) {
			if (dist[nxt]!=-1) continue;
			q.push(nxt);
			dist[nxt]=dist[cur]+1;
		}
	}
}

- BFS 예시 코드 3 : 연결 그래프가 아닐 때 순회

vector<int> adj[10];
bool vis[10];
int v = 9; // 정점의 수
void bfs() {
	queue<int> q;
	for (int i = 1; i <= v; i++) {
		if (vis[i]) continue;
		q.push(i);
		vis[i] = true;
		while (!q.empty()) {
			int cur = q.front();
			q.pop();
			cout << cur << ' ';
			for (auto nxt : adj[cur]) {
				if (vis[nxt]) continue;
				q.push(nxt);
				vis[nxt] = true;
			}
		}
	}
}

[ DFS ]

1. 시작하는 정점을 스택에 넣고 방문했다는 표시를 남김

2. 스택에서 정점을 꺼내어 그 정점과 연결된 모든 정점들에 대해 3번을 진행

3. 해당 정점을 이전에 방문했다면 아무것도 하지 않고, 처음으로 방문했다면 방문했다는 표시를 남기고 해당 칸을 스택에 삽입

4. 스택이 빌 때까지 2번을 반복

- BFS와 같이 모든 정점이 스택에 최대 1번씩 들어가므로 인접 리스트에서 O(V+E), 인접 행렬에서 O(V^2)의 시간 복잡도.

- DFS 예시 코드 1 : 연결 그래프에서의 순회, 비 재귀

vector<int> adj[10];
bool vis[10];
void dfs() {
	stack<int> s;
	s.push(1);
	vis[1] = true;
	while (!s.empty()) {
		int cur = s.top();
		s.pop();
		cout << cur << ' ';
		for (auto nxt : adj[cur]) {
			if (vis[nxt]) continue;
			s.push(nxt);
			vis[nxt] = true;
		}
	}
}

- DFS 예시 코드 2 : 연결 그래프에서의 순회, 재귀

vector<int> adj[10];
bool vis[10];
void dfs(int cur) {
	vis[cur] = true;
	cout << cur << ' ';
	for (auto nxt : adj[cur]) {
		if (vis[nxt]) continue;
		dfs(nxt);
	}
}

- 재귀 함수를 실행하면 점점 Stack 영역에 데이터가 계속 쌓인다.

- 재귀 방법과 비 재귀 방법이 방문하는 순서가 다르다. ( 재귀는 방문 할 때 방문 표시를 남기고, 비재귀는 방문 전에 방문 표시를 남기고 나중에 방문한다 )

- DFS 예시 코드 3 : 연결 그래프에서의 순회, 비재귀 2

vector<int> adj[10];
bool vis[10];
void dfs() {
	stack<int> s;
	s.push(1);
	while (!s.empty()) {
		int cur = s.top();
		s.pop();
		if (vis[cur]) continue;
		vis[cur] = true;
		cout << cur << ' ';
		for (auto nxt : adj[cur]) {
			if (vis[nxt]) continue;
			s.push(nxt);
		}
	}
}

[ 연습문제 ]